A Quick Explanation of Quick Sort

You definitely have heard or read of today’s algorithms in some context or other, whether you’re new to or familiar with sorting algorithms. It tends to precede itself with reputation!

However, what’s quicksort? It’s nice and we could use everyone and the algorithms problem is very well identified! However, some of us — including myself — do not even know what it really is! Time for this to evolve. We need to be well-informed about the in and out of this notorious algorithm if we are to be true algorithm masters!

In this blog, we will take a look at the quick sort algorithm in three folds

1. The logic behind the algorithm

2. Quick sort implementation

3. Quick sort applications

4. Important characteristics and time complexity

5. Advantages and Disadvantages of quick sort

1. The logic behind the algorithm

The Quicksort algorithm is based on the divide and conquer problem-solving method, in which a problem is divided into numerous subproblems, each of which is solved separately, and the final output is the sum of the solutions to each subproblem.

The Divide:

The quick sort algorithm divides an unsorted array of size N into two sections by using an element K as a pivot and maintaining the constraint that all elements in the array to the left of K are less than K and all elements in the array to the right of K are greater than K.

For example: In the array {52, 37, 63, 14, 1 7, 8, 6, 25} ,we take {25} as pivot. which divides the array

The Conquer:

Quick sort returns the pivot element K after dividing the unsorted array into two parts and then partitions each of the two divided parts again. It repeats this process until the unsorted array is partitioned into a sub-array of size 1, at which point it merges all of the elements to produce a sorted array.

2.Quick Sort Algorithm: implementation

1. In the array, look for a “pivot” item. For a single round, this item serves a the comparison point.
2. Start with the first item in the array (the left pointer).
3. Start with the last item in the array (the right pointer).
4. Move the left pointer to the right if the value at the left pointer in the array is less than the pivot value (add 1). Continue until the pivot value is greater or equal to the value at the left pointer.
5. Move the right pointer to the left if the value at the right pointer in the array is greater than the pivot value (subtract 1). Continue until the pivot value is less than or equal to the value at the right pointer.
6. Swap the values at these positions in the array if the left pointer is less than or equal to the right pointer.
7. Move the left pointer one space to the right and the right pointer one space to the left.
8. Return to step 1 if the left and right pointers do not meet.

Below is an image of an array, which needs to be sorted. We will use the Quick Sort Algorithm, to sort this array:

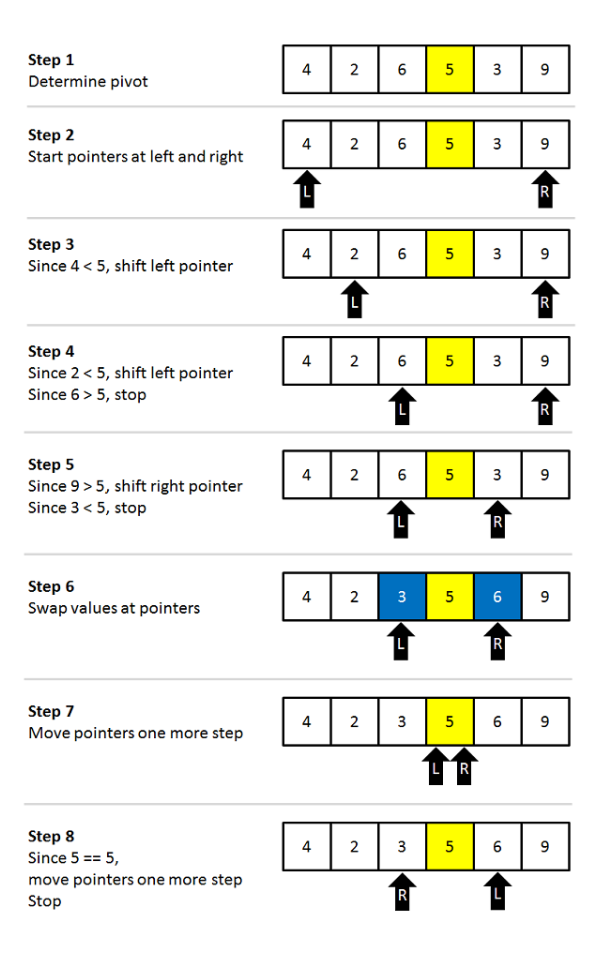
3. Quicksort applications

1. Various programming languages’ internal arrays sort methods are used, such as Javascript primary system sort Array sort method, Java’s collection sort method, and so on.
2. Quick sort is used to arrange sports scores based on the win-loss ratio.
3. In many scientific simulations, the quicksort algorithm is used.
4. In commercial computing, the quicksort algorithm is also widely used.
5. It’s used in things like combinatorics and search.

4.Important Characteristics of Quick Sort:

Quick Sort can be used to sort arrays.

Quick Sort is not a stable sort in effective implementations, which means that the relative order of equal sort items is not maintained.

TIME COMPLEXITY

1. Quick Sort has an overall time complexity of O(nLogn). In the worst-case scenario, it does O(n2) comparisons, though this is uncommon.
2. Quick Sort has an O space complexity (nLogn). It’s an in-place sort (meaning it doesn’t necessitate any additional storage).

5.Advantages and Disadvantages of quick sort

The quick sort is regarded as the best sorting algorithm. This is because of its significant advantage in terms of efficiency because it is able to deal well with a huge list of items. Because it sorts in place, no additional storage is required as well. The slight disadvantage of quick sort is that its worst-case performance is similar to average performances of the bubble, insertion or selections sorts. In general, the quick sort produces the most effective and widely used method of sorting a list of any item size.

Advantages

• It is in-place since it uses only a small auxiliary stack.
• It requires only n (log n) time to sort n items.
• It has an extremely short inner loop.
• This algorithm has been subjected to a thorough mathematical analysis, a very precise statement can be made about performance issues.

Disadvantages

• It is recursive. Especially, if recursion is not available, the implementation is extremely complicated.
• It requires quadratic (i.e., n2) time in the worst-case.
• It is fragile, i.e. a simple mistake in the implementation can go unnoticed and cause it to perform badly.

Resources

Various programming languages rely heavily on Quicksort to implement their sorting algorithms as quickly as possible. As it turns out, there are a lot of resources on this algorithm, and sifting through them all can be a little overwhelming (at least for me!). Here are a few of my favourite places to start if you’re interested in learning more about quick sort.

1. Quicksort algorithm, mycodeschool
2. Sorting Algorithms: QuickSort, Professor Lydia Sinapova
3. Quick Sort, Computerphile
4. Data Structure and Algorithms — Quick Sort, Tutorialspoint
5. QuickSort, GeeksForGeeks
6. Quick Sort in 4 Minutes, Michael Sambol

Conclusion

Overall Quick Sort is an important concept to understand when it comes to algorithms. Thank you for reading this blog post.